〔No. 16〕 誤差伝播
次の文は,トータルステーション(以下「TS」という。)を用いて高低差を求める場合の精度(標準偏差)を計算した過程を示したものである。ア~オに入る数値の組合せとして最も適当なものはどれか。次のページの中から選べ。
ただし,角度1 ラジアンは,(2 ×10⁵)” とする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
TS を用いて,放射法により既知点A から求点B までの高低差を求めるものとする。既知点Aから求点B までの距離をD,高低角をθ,高低差をZ とすると,位置関係は図16 のようになり,高低差Z は式16-1 で表される
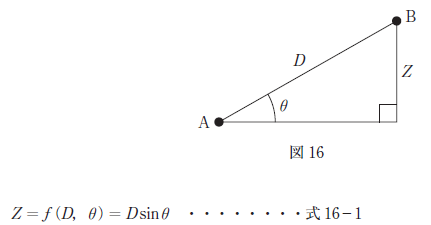
ここで,斜距離D,高低角θ それぞれの観測値の標準偏差をσD,σθ とした場合の,高低差Z の標準偏差σZ を求めることにする。
ただし,既知点A から求点B を観測した測定値は,斜距離の測定距離D₀=100.000 m,高低角θ₀ =30°00’ 00″,使用したTS の距離測定の精度(標準偏差)は(5 +5 ×10⁻⁶D)mm(D はmm 単位の測定距離),角度測定の精度(標準偏差)を5″ とする。
また,TS による距離測定と角度測定は互いに影響を与えないものとし,その他の誤差は考えないものとする。
斜距離D と高低角θ の観測が互いに独立であることから,両者の共分散は0 となる。それぞれの観測値の分散をσD²,σθ² とした場合,高低差Z の分散σZ² は,誤差伝播の法則から式16-2 で
求められる。
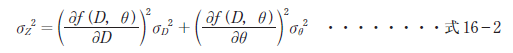
D =D₀,θ=θ₀ のときの具体的な数値は,距離の単位をmm,角度の単位をラジアンとすると次のように計算できる。
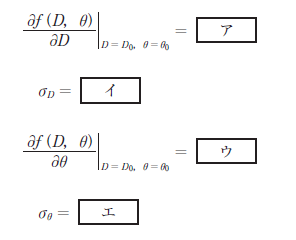
これらを式16-2 に代入し,高低差Z の標準偏差σZ を計算すると,
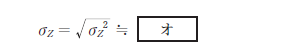
となる。

高低差の標準偏差、誤差伝播を求める虫食い問題じゃ🐞
問題自体は全く分からなかったのじゃが、∂で偏微分が必要なのが分かったので近代経済学でさんざん使った微分を使ったぞ。
Z=D・sinθをDで偏微分をするとDは消えるので……
∂D=sinθ
∂D=0.5 [ア]
斜距離の標準偏差は(5 +5 ×10⁻⁶D)mmなので……
σD=5mm+5 ×10⁻⁶×100000mm=5.5mm [イ]
Z=D・sinθをθで偏微分をするとsinθはcosθになるので……
∂θ=D・cosθ
今まで上述はmmで計算しているので、mmに単位を合わせて……
∂θ=100.000m×cos30°=100000mm×0.86603=86603 [ウ]
角度測定の標準偏差が5″なので、方向角の標準偏差は……
σθ=5″/(2 ×10⁵)” =0.000025mm [エ]
この時点で肢3が正答ということが分かるけど、念のため[オ]も……
式16-2に代入するよ🎶
σZ=√[(0.5×5.5)²+(86603×0.000025)²]≒3.5mm [オ]

[オ]は電卓を理解していれば簡単に計算ができるよ🔢
電卓の操作も紳士が埼玉県立常盤高等学校の看護専攻科の統計学で教えていたのじゃ。
会場で渡される電卓はCASIO SL-910GT-Nなので……
[MC]0.5[×]5.5[×][×][M+]86603[×]0.000025[×][×][M+][MR][√]
……で3.5000069と一発で出るのじゃ🎉
もしくは……
[MC]0.5[×]5.5[×][M+]86603[×]0.000025[×][M+][MR][√]
でも、わらわは[×][×]派じゃ🔣
[MC]はメモリクリアで、前の計算の数値が残っているといけないので、念のためのおまじないとして最初に押しておくぞ。画面に『M』が表示されていたら必須操作じゃ。
[M+]はメモリプラスで直線の計算結果を加えますというボタンじゃ。
[MR]はメモリリコールで記録したメモリの合計を足してくれるぞ。
2乗は[×]でも[×][×]でも出来るぞ。
[×][×]だと定数計算モードになって『K』と画面に表示されるよ。
ただの……このモードになったら[=]を連打するとどんどん計算するから注意するがよい❎
じゃぁ、計算していくぞ❗
メモリをおまじないでクリアして、0.5×5.5をかけかけで2乗……

エムプラス……

86603×0.000025をかけかけで2乗してエムプラス……

エムイコール……

ルートは❓

という感じじゃ🎊
秒で計算が終わるからお勧めだぞ。