
〔No. 5〕 法規
100点を満点とするある試験において,受験者の点数の分布が近似的に平均60点,標準偏差10点の正規分布に従うことが分かった。この試験は1,000人が受験し,上位3%が合格する。この試験の最低合格点は幾らか。最も近いものを次のページの中から選べ。
ただし,必要に応じて表5 の値を用いよ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
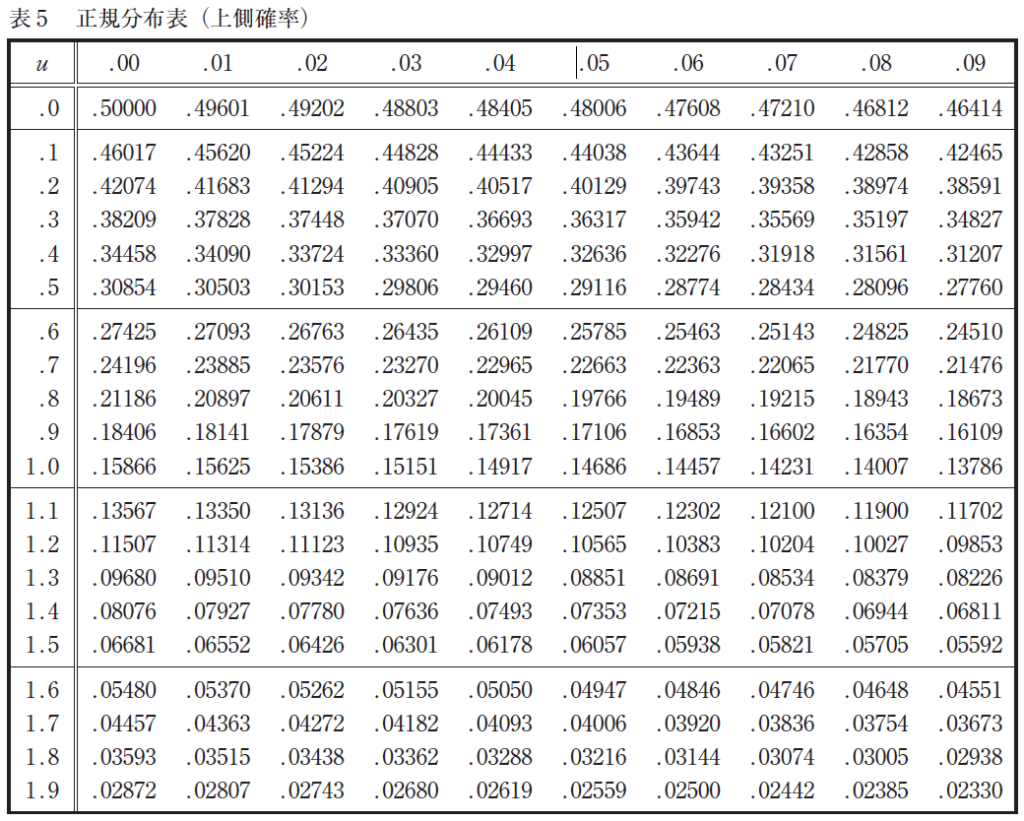
表5 は𝜇=0.00~1.99に対する,標準正規分布の正規分布表(上側確率)である。
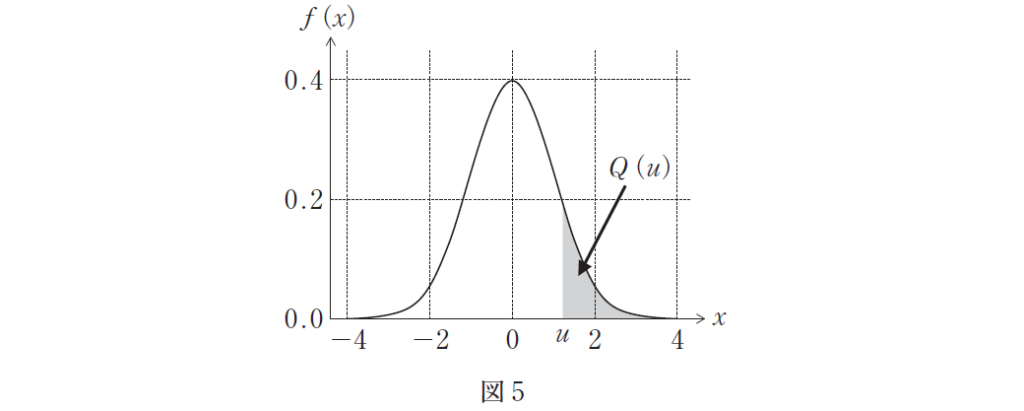
また,標準正規分布の確率密度関数𝑓(𝑥) の上側確率Q(𝜇) は式5 で表される。
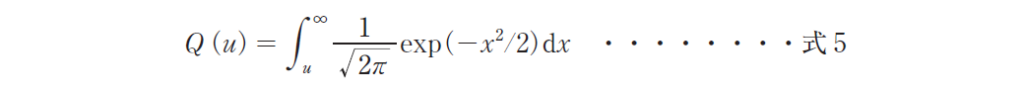
これは図5 の着色部の面積にあたる。
例:𝜇=1.23に対する上側確率Q(𝜇) は,表5 の左の見出しから小数第1 位までの1.2と,上の見出しから小数第2位の.03とが交差するところで,Q(𝜇)=0.10935が得られる。

統計の問題に見えるが、中・高校生だと統計というより確率の問題なのじゃ。
わらわは得意というか、いわゆる看護高専の埼玉県立常盤高等学校の看護専攻科に教えていた専門の統計学じゃ🎶
一般の正規曲線で平均𝜇 、標準偏差𝜎 の横軸上の任意の点𝑥 を、 標準正規曲線の横軸上の一点、規準正規変数𝑧 に対応させる関係は、
𝑥=𝜇+𝑧𝜎
標準化した𝑧 は
𝑧=(𝑥-𝜇)/𝜎
これにより、正規曲線の全ての確率変数𝑥 の値は標準正規曲線、すなわち表5の正規分布表の対応値で表せるようになるぞ。
受験者の得点を𝑥 、合格の最低点をαとすれば、P(𝑥 ≥ α) = 0.03が成り立つので、
𝑥~N(60 , 10²)だから
P[𝑧≥ (αー60) /10 ]=0.03
ここで、 𝑧 ∼ N(0, 1) なので表5の正規分布表から、P(𝑧 ≥ 1.88) = 0.03くらいであるから、求める αは……
(α-60)/10=1.88
α=78.8

難しいことは抜きじゃ❗
PowerPointで[Σ]と表示した瞬間に「看護科の時にシグマの公式をきちんと教わっていない」とブーイングが出た看護専攻科で教えたようにお伝えするのじゃ🎵
① 上位3%が合格するので、これを少数にすると0.03じゃの。
3/100=0.03
② 標準正規分布の正規分布表(上側確率)から0.03を探すぞ🔍
ただ、0.03はないので近いところを探すと0.03005が一番いい感じじゃ。
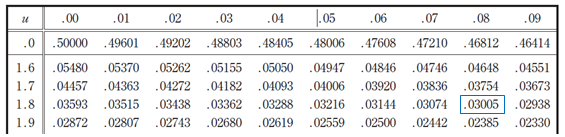
③ 𝑧 は1.8と0.08なので1.88と読み取るぞ🔢
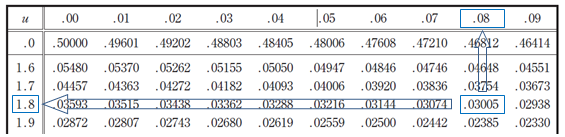
④ でも最後は標準化の公式を変形して算出するしかないのじゃ💧
𝑧=(𝑥-𝜇)/𝜎
確率変数𝑥 を標準化した𝑧 =(個々のデーター平均)/標準偏差
1.88=(𝑥-60)/10
𝑥=78.8
∴ 最低合格点は79点





